Kita berjumpa lagi kawan 😁😁
Kali ini pembahasannya melanjutkan pembahasan yang kemarin ya
➢Pertaksamaan kuadrat
1. Selesaikan ketaksamaan kuadrat berikut x²-x<6
#langkah pertama adalah memindahkan ruas kanan kekiri dan memfaktorkannya
X²-X-6<0
(x-3)(x+2)<0
x=3 atau x=-2
#langkah kedua kira pecah nilai x menjadi 3 selang ya (-~,-2)(-2,3)(3,~)
Nb:cara pemecahannya bilangan x terkecil maka ibaratkan dia kurang dari x (x<-2), dan bilangan x terbesar ibaratkan lebih dari x (x>3)
Paham kan?
#setelah kita pecah jadi 3 maka kita uji kan ke dalam persamaan agar kita bisa menentukan nilai hasilnya positif atau negatif. Berikut gambarnya
Setelah kita uji, ternyata hasilnya positif, negatif, positif. Maka HP nya adalah (-2,3)
2. Selesaikanlah 3x²-x-2>0
#karena persamaan sudah dipindah ruas maka tinggal kita faktorkan terlebih dahulu
(3x+2)(x-1)
x=-2/3 atau x= 1
#kita pecah menjadi 3 selang (-~,-2/3) (-2/3,1)(1,~)
#ujikan pada titik" yang ada disekitanya bilangan sembarang. Berikut gambarnya
Dapat kita simpulkan bahwa HP nya berada dalam selang (-~,-2/3) dan (1,~) . Dalam bahasa himpunan, HP nya adalah gabungan (dilambangkan dengan U) dari dua selang tersebut (-~,-2/3) U (1,~).
Lanjut pada materi berikutnya ya.
Lanjut pada materi berikutnya ya.
Yaitu Nilai Mutlak, ini juga materi precalculus yang harus kita ketahui ya.

Nilai Mutlak suatu bilangan real x dinyatakan dengan |x|, didefinisikan sebagai
1. |x| =x jika x>=0
2. |x| =-x jika x<0

Nilai Mutlak suatu bilangan real x dinyatakan dengan |x|, didefinisikan sebagai
1. |x| =x jika x>=0
2. |x| =-x jika x<0
Definisi tanda nilai mutlak ini juga harus dikaji dengan seksama, karena ada benarnya bahwa |x| selalu tak negatif, adalah benar juga bahwa |-x|=|x|
Sifat-sifat nilai mutlak
1. |ab|=|a| |b|
2. |a/b|=|a/b|
3. |a+b| <=|a|+|b|
4. |a-b|>=|a|-|b|
Sifat-sifat nilai mutlak
1. |ab|=|a| |b|
2. |a/b|=|a/b|
3. |a+b| <=|a|+|b|
4. |a-b|>=|a|-|b|
Contoh soal nilai mutlak yang melibatkan ketaksamaan
1. Selesaikanlah ketaksamaan |x-4|<2
Jawab:
gunakan rumus |x|<a <=> -a<x<a
|x-4|<2 <=> -2<x-4<2
untuk menghilangkan -4 atau mencari nilai x maka kita harus menambah ruas kanan kiri dan tengah dengan angka 4 dan hasilnya 2<x<6.
2. Selesaikan persamaan: –5|x – 7| + 2 = –13.
Pembahasan Pertama, kita isolasi nilai mutlak, yaitu membuat simbol nilai mutlak berada pada satu ruas sedangkan suku-suku lainnya kita letakkan di ruas yang lain.
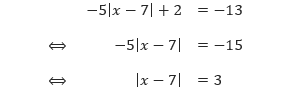
Sekarang perhatikan bahwa x – 7 merupakan “X” pada sifat persamaan nilai mutlak, sehingga

Dengan mensubstitusi ke persamaan semula akan memastikan bahwa himpunan selesaiannya adalah {4, 10}.
Catatan Untuk persamaan seperti pada contoh 1 di atas, hati-hati untuk tidak memperlakukan simbol nilai mutlak seperti tanda kurung biasa. Persamaan –5(x – 7) + 2 = –13 hanya memiliki selesaian x = 10, dan tidak memiliki selesaian kedua karena persamaan tersebut memiliki bentuk sederhana x – 7 = 3. Persamaan –5|x – 7| + 2 = –13 dapat disederhanakan menjadi |x – 7| = 3 yang memiliki dua selesaian.
Persamaan nilai mutlak dapat muncul dari berbagai bentuk. Tetapi dalam menyelesaikan persamaan tersebut, kita harus mengisolasi simbol nilai mutlak baru kemudian menerapkan sifat persamaan nilai mutlak.
3. Tentukan himpunan selesaian dari persamaan: |5 – 2/3 x| – 9 = 8.
Pembahasan Dengan mengisolasi simbol nilai mutlak baru kemudian menerapkan sifat persamaan nilai mutlak, kita mendapatkan
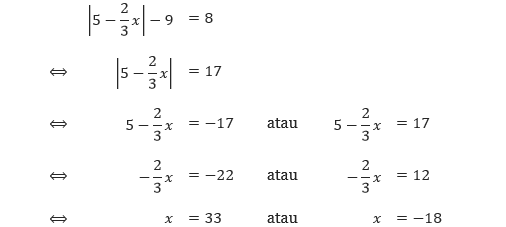
Sehingga, himpunan selesaian dari persamaan tersebut adalah {–18, 33}.
4. Himpunan penyelesaian dari persamaan |2x + 3| = |x + 6| adalah ...
jawab
|2x + 3| = |x + 6|
(2x + 3)² = (x + 6)²
4x² + 12x + 9 = x² + 12x + 36
3x² - 27 = 0
x² - 9 = 0
(x + 3)(x - 3) = 0
x = -3 atau x = 3
HP = {-3, 3}
5. Tentukan nilai x dari |3x+2|²+|3x+2|-2=0
Penyelesaian :
Misal : |3x+2| = p
maka
|3x+2|²+|3x+2|-2=0
p² + p – 2 = 0
(p+2) (p-1) = 0
p+2 = 0
p = -2 (nilai mutlak tidak negatif )
atau
p-1 = 0
p = 1
|3x+2| = 1
=> 3x+2 = 1
3x = 1-2
3x = -1
x = -1/3
=> -(3x+2) = 1
3x+2 = -1
3x = -1-2
3x = -3
x = -1
Jadi penyelesaiannya adalah x=-1/3 atau x=-1
sumber
http://rumus-matematika.com/contoh-soal-dan-penyelesaian-nilai-mutlak/
sekian dulu kawan
dibahas lain hari ya, soalnya disini admin lagi nggak enak badan dan susah jaringannya hehehe



Tidak ada komentar:
Posting Komentar