Assalamu'alaikum wr. wb
selamat jumpa kembali pada blog saya
materi kali ini limit fungsi ya
limit f(x)=L
x-->a
Limit x suatu fungsi merupakan salah satu konsep mendasar dalam kalkulus dan analisis, tentang kelakuan suatu fungsi mendekati titik masukan tertentu.
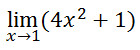
Jawab :Untuk nilai x mendekati 1 maka (4x2+1) akan mendekati 4.12 + 1 = 5 sehingga nilai dari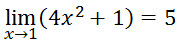
Contoh 2Tentukan nilai dari limit
Misal langsung memasukkan nili x = 1 ke dalam persamaan hasilnya tidak akan terdefinisi karena bilangan pembagi ketemu 0 (x-1). Akan tetapi bentuk di atas masih bisa disederhakan guna menghilangkan komponen pembagi yang bernilai nol yaitu

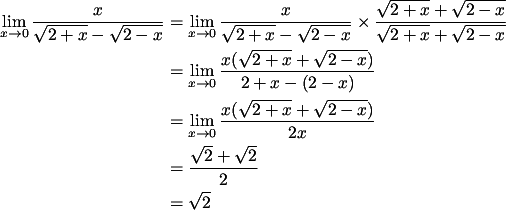


jawab:

cara diatas merupakan cara turunan dalam menyelesaikan soal limit fungsi
sumber :
selamat jumpa kembali pada blog saya
materi kali ini limit fungsi ya
limit f(x)=L
x-->a
Limit x suatu fungsi merupakan salah satu konsep mendasar dalam kalkulus dan analisis, tentang kelakuan suatu fungsi mendekati titik masukan tertentu.
- Limit searah
Masukan x dapat mendekati p dari atas (kanan di garis bilangan) atau dari bawah (kiri). Dalam hal ini limit masing-masingnya dapat ditulis sebagai
atau
Bila kedua limit ini sama nilainya dengan L, maka L dapat diacu sebagai limit f(x) pada p . Sebaliknya, bila keduanya tidak bernilai sama dengan L, maka limit f(x) pada p tidak ada.
Definisi formal adalah sebagai berikut. Limit f(x) saat x mendekati p dari atas adalah L bila, untuk setiap ε > 0, terdapat sebuah bilangan δ > 0 sedemikian rupa sehingga |f(x) - L| < ε pada saat 0 < x - p < δ. Limit f(x) saat x mendekati p dari bawah adalah L bila, untuk setiap ε > 0, terdapat bilangan δ > 0 sehingga |f(x) - L| < ε bilamana 0 < p - x < δ.
Bila limitnya tidak ada terdapat osilasi matematis tidak nol.
contoh soal limit
Contoh 1
Tentukan limit dari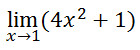
Jawab :Untuk nilai x mendekati 1 maka (4x2+1) akan mendekati 4.12 + 1 = 5 sehingga nilai dari
Contoh 2Tentukan nilai dari limit
Misal langsung memasukkan nili x = 1 ke dalam persamaan hasilnya tidak akan terdefinisi karena bilangan pembagi ketemu 0 (x-1). Akan tetapi bentuk di atas masih bisa disederhakan guna menghilangkan komponen pembagi yang bernilai nol yaitu
Jawab
note: untuk limit fungsi ke a bagian polynomial maka langsung disubstitusikan
kecuali jika mendapat bentuk tak tentu seperti dibawah ini
Adakalanya penggantian nilai x oleh a dalam lim f(x) x→a membuat f(x) punya nilai yang tidak terdefinisi, atau f(a) menghasilkan bentuk 0/0, ∞/∞ atau 0.∞. Jika terjadi hal tersebut solusinya adalah bentuk f(x) coba disederhanakan agar nilai limitnya dapat ditenntukan.
Limit Bentuk 0/0
contohnya
jika disubstitusikan awalnya akan menjadi 1-1/1-1=0/0
Bentuk ∞/∞
Bentuk limit ∞/∞ terjadi pada fungsi suku banyak (polinom) seperti
Contoh Soal
Jawab
- Jika m<n maka L = 0
- Jika m=n maka L = a/p
- Jika m>n maka L = ∞
Bentuk Limit (∞-∞)
Tentukan Limit
Jika memasukkan x -> 1 maka bentuknya akan mmenjadi (∞-∞). Untuk menghilangkan bentuk ∞-∞ kita sederhanakan bentuk tersebut menjadi
Dari cara diatas dapat kita simpulkan bahwa metode pengerjaan soal limit adalah
1. disubstitusikan langsung
2. jika mendapat bentuk tak tentu maka harus difaktorkan dahulu
sekarang kita coba metode yang lain
contoh soal

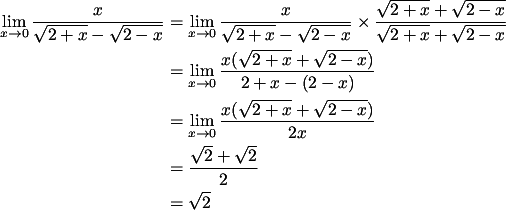
cara diatas merupakan cara ketiga dalam menyelesaikan soal limit yaitu pengalian dengan sekawannya

jawab:



jawab:

cara diatas merupakan cara turunan dalam menyelesaikan soal limit fungsi
sumber :
http://pengetahuan-olandsky.blogspot.com/2013/11/contoh-soal-limit-fungsi-matematika.html
https://maths.id/limit-dengan-pemfaktoran-dan-perkalian-sekawan.ph
https://rumushitung.com/2014/03/02/limit-matematika-dan-contoh-so
https://id.wikipedia.org/wiki/Limit_fungsi
sekian dulu kawan
semoga bermanfaat
assalamu'alaikum wr. wb.
https://maths.id/limit-dengan-pemfaktoran-dan-perkalian-sekawan.ph
https://rumushitung.com/2014/03/02/limit-matematika-dan-contoh-so
https://id.wikipedia.org/wiki/Limit_fungsi
sekian dulu kawan
semoga bermanfaat
assalamu'alaikum wr. wb.




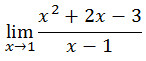
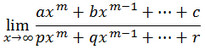
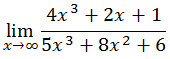
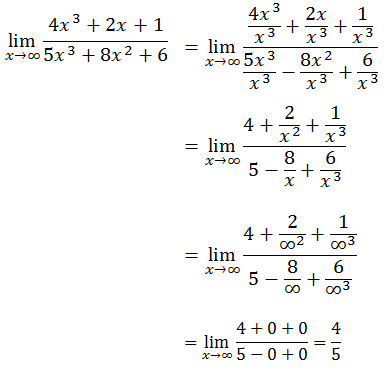

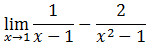
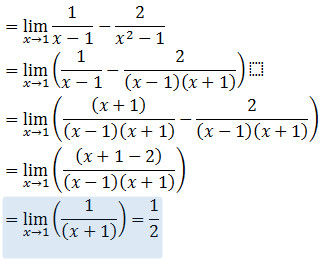
Tidak ada komentar:
Posting Komentar