Assalamu'alaikum wr. wb.
Selamat datang di blog saya lagiiiiiiii✰✰✰✰✰✰✰✰✰✰✰❤

lanjut pada bentuk'' eksponen gaiss
f(3) = 23+1 = 24 = 16
f(-3) = 2-3+1 = 2-2 = 1/4 = 0,25
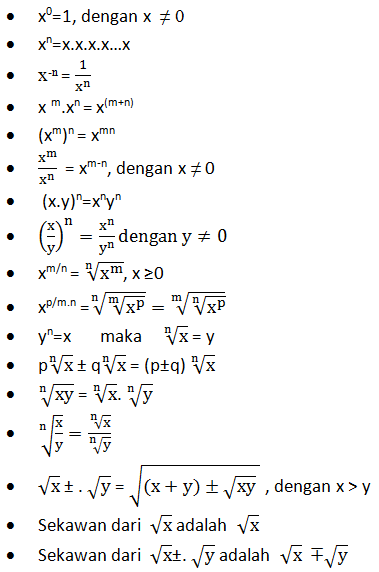
HEMMM...hemmm
gimana?
gimana?
yak pembahasan kali ini cukup mengasyikan ya kawan, eksponen? tentunya udah terdefinisi yaa apa itu eksponen. dan udah admin cantumkan sekalian RANGKUMANNYA. JADII ❤❤❤❤❤❤❤❤
Selamat datang di blog saya lagiiiiiiii✰✰✰✰✰✰✰✰✰✰✰❤

Pengertian eksponen
Definisi eksponen adalah nilai yang menunjukkan derajat kepangkatan (berapa kali bilangan tersebut dikalikan dengan bilangan tesebut juga). Bentuk an (baca: a pangkat n) disebut bentuk eksponensial atau perpangkatan. a disebut dengan bilangan pokok (basis) dan n disebut eksponennya. Jika n adalah bilangan bulat positif maka definisi dari eksponen
an = a x a x a x ….. x a (a sejumlah n faktor)
contoh : 34 = 3 x 3 x 3 x 3 = 81
dalam
eksponen, bilangan pangkat tidak selamanya selalu bernilai bulat
positif tetapi dapat juga bernilai nol, negatif, dan pecahan.lanjut pada bentuk'' eksponen gaiss
Eksponen (pangkat) nol
Jika a ≠ 0 maka a0 = 1
contoh
10 =1
20 =1
1283840 =1
x0 =1
Semua bilangan yang dipangkatkan 0 hasilnya adalah 1
kecuali 0.
contoh
10 =1
20 =1
1283840 =1
x0 =1
Semua bilangan yang dipangkatkan 0 hasilnya adalah 1
kecuali 0.
Eksponen (pangkat) negatif dan pecahan
Jika m dan n adalah bilangan bulat positif maka
(i) a-n = 1/an
contoh
2-3 = 1/23 = 1/8
(ii) a1/n = n√a
contoh
21/2 = √2
21/3 = 3√2
Setelah teman-teman berkenalan dengan eksponen, kita lanjut ke sifat-sifatnya.
(i) a-n = 1/an
contoh
2-3 = 1/23 = 1/8
(ii) a1/n = n√a
contoh
21/2 = √2
21/3 = 3√2
Setelah teman-teman berkenalan dengan eksponen, kita lanjut ke sifat-sifatnya.
Sifat-sifat Eksponen
- am . an = am+n
Jika kalian punya bilangan dasar sama dengan pangkat berbeda maka hasil perkaliannya adalah bilangan dasar dengan pangkat hasil penjumlahan pangkat masing-masing bilangan.
Contoh:
x4 . x6 = x(4+6) = x10
74 . 7-2 = 7(4-2) = 72 - am/an = am-n
Kebalikan dari sift pertama kalau bilangan dasar yang sama membagi salah satu, maka pangkatnya dikurangi
Contoh:
x1/2 : x1/4 = x(1/2-1/4) = x1/4 - (am)n = amn
Suatu bilangan berpangkat jika dipangkatkan lagi maka pangkat akhirnya adalah perkalian pangkatnya
Contoh:
(32)3 = 32.3 = 36 - (am.bn)p = amp. bnp
Contoh:
(x2.y3)2 = x2.2 . y3.2 = x4.y6 - (am/an)p = amp/anp
Contoh
(23/24)3 = 23.3/24.3

- BENTUK PERSAMAAN EKSPONEN
1. af(x) = 1 ( Jika af(x) = 1 dengan a>0 dan a ≠0, maka f(x) = 0 )
2. af(x) = ap ( Jika af(x) = ap dengan a>0 dan a ≠0, maka f(x) = p )
3. af(x) = ag(x) ( Jika af(x) = ag(x) dengan a>0 dan a ≠0, maka f(x) = g(x) )
4. af(x) = bf(x) ( Jika af(x) = bf(x) dengan a>0 dan a ≠1, b>0 dan b ≠1, dan a≠b maka f(x) = 0 )
5. A(af(x))2 + B(af(x)) + C = 0 ( Dengan af(x) = p, maka bentuk persamaan diatas dapat diubah menjadi persamaan kuadrat : Ap2 + Bp + C =
Contoh Soal Persamaan Eksponen Bentuk af(x) = 11. Tentukan himpunan penyelesaiian dari :a. 3 5x-10 = 1b. 2 2x²+3x-5 = 1Jawab :a. 3 5x-10 = 13 5x-10 = 305x-10 = 05x = 10x = 2
b. 2 2x²+3x-5 = 12 2x²+3x-5 = 202x2+2x-5 = 0(2x+5) (x-1) = 02x+5 = 0 | x-1 = 0X = -²⁄₅ | x = 12. Contoh Soal Persamaan Eksponen Bentuk af(x) = apTentukan himpunan penyelesaian dari :a. 5 2x-1 = 625b. 2 2x-7 = ⅓₂c. √33x-10 = ½₇√3Jawab :a. 5 2x-1 = 6255 2x-1 = 532x-1 = 32x = 4x = 2
b. 2 2x-7 = ⅓₂2 2x-7 = 2-52x-7 = -52x = 2x = 1
c. √33x-10 = ½₇√333x-10⁄2 = 3-3.3½33x-10⁄2 = 3-⁵⁄₂3x-10⁄2 = -⁵⁄₂3x-10 = -53x = 5x = ⁵⁄₃3. Contoh Persamaan Eksponen Bentuk af(x) = ag(x)Tentukan himpunan penyelesaian dari :a. 9 x²+x = 27 x²-1b. 25 x+2 = (0,2) 1-xJawab :a. 9 x²+x = 27 x²-13 2(x²+x) = 3 3(x²-1)2 (x2+x) = 3 (x2-1)2x2 + 2x = 3x2 – 3x2 – 2x – 3 = 0(x – 3) (x + 1) = 0x = 3 x = -1 Jadi HP = { -1,3 }b. 25 x+2 = (0,2) 1-x52(x+2) = 5 -1(1-x)2x + 4 = -1 + x2x – x = -1 – 4x = -5 Jadi HP = { -5 }4. Contoh Persamaan Eksponen Bentuk af(x) = bf(x)Tentukan himpunan penyelesaian dari :a. 6 x-3 = 9 x-3b. 7x²-5x+6 = 8x²-5x+6Jawab :a. 6 x-3 = 9 x-3x-3 = 0x = 3Jadi HP = { 3 }b. 7x²-5x+6 = 8x²-5x+6x²-5x+6 = 0(x-6) (x+1) = 0x = 6 x = -1Jadi HP = { -1,6 }5. Contoh Persamaan Eksponen Bentuk A(af(x))2 + B(af(x)) + CTentukan himpunan penyelesaian dari :a. 22x – 2x+3 + 16 = 0Jawab :a. 22x – 2x+3 + 16 = 022x – 2x.23 + 16 = 0Misalkan 2x = p, maka persamaannya menjadiP2 – 8p + 16 = 0(p-4) p-4) = 0p = 4Untuk p = 4, jadi2x = 42x = 22x = 2
Jadi HP = { 2 }
Fungsi Eksponen dan Grafiknya
fungsi
eksponene merupakan pemetaan bilangan real x ke ax dengan a > 0 dan
a ≠ 1. Jika a > dan a ≠ 1, x ∈ R maka f:(x) = ax disebut sebagai
fungsi eksponen.
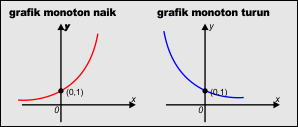
Fungsi eksponen y = f(x) = ax; a> 0 dan a ≠ 1 mempunyai sifat-sifat
Fungsi eksponen y = f(x) = ax; a> 0 dan a ≠ 1 mempunyai sifat-sifat
- Kurva terletak di atas sumbu x (definit positif)
- memotong sumbu y di titik (0,1)
- mempunyai asimto datar y = 0 (sumbu x)
- grafik monoton naik untuk x > 1
- grafik berbentuk monoton turun untuk 0<x<1
Contoh Soal:
Jika f(x) = 2x+1 tentukan nilai dari f(3) dan f(-3)f(3) = 23+1 = 24 = 16
f(-3) = 2-3+1 = 2-2 = 1/4 = 0,25
Persamaan Fungsi Eksponen
ada beberapa bentuk persamaan eksponen diantaranya adalah
(i) jika af(x) = ap maka f(x) = p
(ii) jika af(x) = ag(x) maka f(x) = g(x)
(i) jika af(x) = ap maka f(x) = p
(ii) jika af(x) = ag(x) maka f(x) = g(x)
Contoh Soal
tentukan nilai dari x agar 32x-3 = 0
jawab
32x-3 = 0
32x =31
2x = 1 maka x = 1/2
tentukan nilai dari x agar 32x-3 = 0
jawab
32x-3 = 0
32x =31
2x = 1 maka x = 1/2
tentukan nilai x dari persamaan 35x-1 – 27x+3 = 0
jawab
35x-1 – 27x+3 = 0
35x-1 = (33)x+3
35x-1 = 33x+9
5x-1 = 3x + 9
2x = 10
x = 5
jawab
35x-1 – 27x+3 = 0
35x-1 = (33)x+3
35x-1 = 33x+9
5x-1 = 3x + 9
2x = 10
x = 5
cari himpunan penyelesaian dari persamaan eksponen 32x+2 + 8.3x -1 = 0
jawab
32x+2 + 8.3x -1 = 0 untuk memudahkan mengerjakannya sobat bisa memisalkan 3x = a
32x+2 + 8.3x -1 = 0
32x 32+ 8.3x -1 = 0
(3x)2 32+ 8.3x -1 = 0
9a2 + 8a -1 = 0 kita faktorkan persamaan kuadrat tersebut
(9a-1)(a+1) = 0
9a-1 = 0
9a = 1
a = 1/9
atau
a + 1 = 0
a = -1
kembali ke permisalan awal 3x = a
3x = 1/9 maka x = -2
3x = -1 (tidak memenuhi) jadi nilai x yang memenuhi adalah -2
RANGKUMAN EKSPONEN
jawab
32x+2 + 8.3x -1 = 0 untuk memudahkan mengerjakannya sobat bisa memisalkan 3x = a
32x+2 + 8.3x -1 = 0
32x 32+ 8.3x -1 = 0
(3x)2 32+ 8.3x -1 = 0
9a2 + 8a -1 = 0 kita faktorkan persamaan kuadrat tersebut
(9a-1)(a+1) = 0
9a-1 = 0
9a = 1
a = 1/9
atau
a + 1 = 0
a = -1
kembali ke permisalan awal 3x = a
3x = 1/9 maka x = -2
3x = -1 (tidak memenuhi) jadi nilai x yang memenuhi adalah -2
RANGKUMAN EKSPONEN
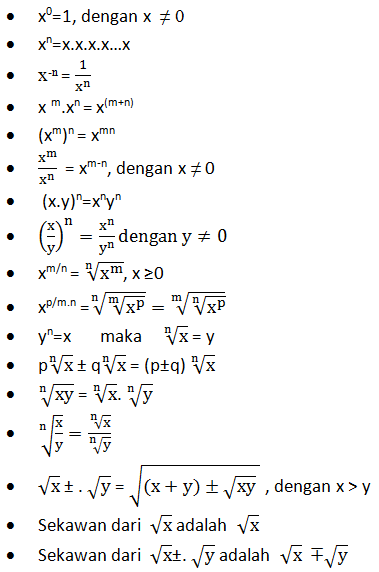
HEMMM...hemmm
gimana?
gimana?
yak pembahasan kali ini cukup mengasyikan ya kawan, eksponen? tentunya udah terdefinisi yaa apa itu eksponen. dan udah admin cantumkan sekalian RANGKUMANNYA. JADII ❤❤❤❤❤❤❤❤
sumber:
https://tanya-tanya.com/rangkuman-contoh-soal-pembahasan-eksponen-logaritma/
http://rumusdasarmatematika.blogspot.com/2014/10/persamaan-eksponen-dan-contoh-soal.html
https://rumushitung.com/2013/09/18/eksponen-matematika-sma/
https://tanya-tanya.com/rangkuman-contoh-soal-pembahasan-eksponen-logaritma/
http://rumusdasarmatematika.blogspot.com/2014/10/persamaan-eksponen-dan-contoh-soal.html
https://rumushitung.com/2013/09/18/eksponen-matematika-sma/


Tidak ada komentar:
Posting Komentar